219. En un
sistema de referencia cartesiano con origen de coordenadas $\left( 0,0 \right)$,
un peatón sigue la trayectoria de la recta que pasa por los puntos $A\ \left(
2,0 \right)$ y $B\ \left( 5,2 \right)$ mientras que otro peatón sigue la
trayectoria de la recta que pasa por los puntos $C\ \left( 1,3 \right)$ y $D\
\left( -3,-1 \right)$. Entonces, la ordenada del punto donde se cortan las
trayectorias de ambos peatones es
a) la
trayectoria de ambos peatones no se corta en ningún punto
b) -8
c) 15
Si las
trayectorias son rectas tendrán de ecuación $y=mx+n$ donde m es la pendiente de la recta (mide la
inclinación) y n es la ordenada en el
origen (indica el punto de corte de la recta con el eje vertical de
ordenadas).
Calculemos
primero la ecuación de la trayectoria del primer peatón, la recta que pasa por
los puntos $A\ \left( 2,0 \right)$ y $B\ \left( 5,2 \right)$:
si la
recta pasa por el punto $\left( 2,0 \right)$, las coordenadas del punto deben
cumplir la ecuación de la recta: $0=m\times (2)+n\quad \Rightarrow \quad
0=2m+n$
igualmente
si pasa por el punto $\left( 5,2 \right)$, las coordenadas del punto deben
cumplir la ecuación de la recta: $2=m\times (5)+n\quad \Rightarrow \quad
2=5m+n$.
Como pasa
por ambos puntos, deben cumplirse ambas condiciones y obtenemos un sistema de
ecuaciones cuya solución nos dará los valores de m y n:
y
sustituyendo en alguna de las ecuaciones:
$0=2m+n\quad \Rightarrow \quad
0=2\times \frac{2}{3}+n\quad \Rightarrow \quad 0=\frac{4}{3}+n\quad \Rightarrow
$
Por lo que
la ecuación de la recta que pasa por los puntos $A\ \left( 2,0 \right)$ y $B\
\left( 5,2 \right)$ es:
$y=mx+n\quad
\Rightarrow \quad y=\frac{2}{3}x-\frac{4}{3}$
De igual
manera calcularemos la ecuación de la recta que pasa por los puntos $C\ \left(
1,3 \right)$ y $D\ \left( -3,-1 \right)$:
si la
recta pasa por el punto $\left( 1,3 \right)$, las coordenadas del punto deben
cumplir la ecuación de la recta: $3=m\times (1)+n\quad \Rightarrow \quad 3=m+n$
igualmente
si pasa por el punto $\left( -3,-1 \right)$, las coordenadas del punto deben
cumplir la ecuación de la recta: $-1=m\times (-3)+n\quad \Rightarrow \quad
-1=-3m+n$.
Como pasa
por ambos puntos, deben cumplirse ambas condiciones y obtenemos un sistema de
ecuaciones cuya solución nos dará los valores de m y n:
y
sustituyendo en alguna de las ecuaciones:
Por lo que
la ecuación de la recta que pasa por los puntos $C\ \left( 1,3 \right)$ y $D\
\left( -3,-1 \right)$ es:
$y=mx+n\quad
\Rightarrow \quad y=1x+2\quad \Rightarrow \quad y=x+2$
Analizando
las ecuaciones de las dos rectas, $y=\frac{2}{3}x-\frac{4}{3}$ y $y=x+2$, se
observa que la pendiente de la primera es $m=\frac{2}{3}$ y la pendiente de la
segunda es $m'=1$, es decir, las pendientes son distintas, por lo que las dos
rectas no son paralelas y se cortarán en algún punto: el punto de corte de las
dos trayectorias que estábamos buscando.
Para
calcular las coordenadas $\left( x,y \right)$ de dicho punto de corte hay que
recordar que será un punto que pertenezca a ambas rectas, es decir, que cumpla
ambas ecuaciones, es decir, que sea solución del sistema formado por ambas
ecuaciones:
$\Rightarrow \quad
\frac{2x}{3}-\frac{3x}{3}=\frac{6}{3}+\frac{4}{3}\quad \Rightarrow \quad
\frac{-x}{3}=\frac{10}{3}\quad \Rightarrow $
Y la
ordenada de dicho punto será, sustituyendo en cualquiera de las ecuaciones:





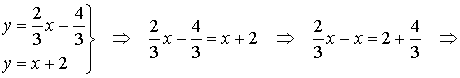



No hay comentarios:
Tu opinión importa, deja un comentario o anota tus dudas