481. Sean los conjuntos $A=\left\{ a,b,c \right\}$, $B=\left\{ 1,2,3 \right\}$, y $f:A\to B$ la transformación $f(a)=1$; $f(b)=3$; $f(c)=2$. Entonces

a) $f$ es aplicación

b) ${{f}^{-1}}(\left\{ 2,3 \right\})=\left\{ a,c \right\}$

c) ${{f}^{-1}}(\left\{ 1,3 \right\})=\left\{ a,c \right\}$

 

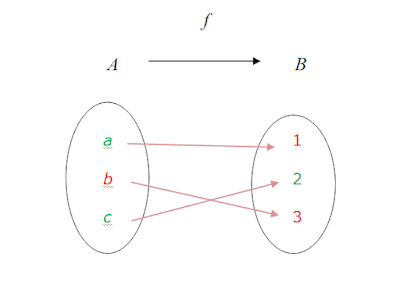
La representación gráfica de la transformación definida quedaría:

Para que sea aplicación, todos los elementos del conjunto inicial deben tener “una y solo una” imagen en el conjunto final (es decir, de todos y cada uno de los elementos del conjunto inicial debe salir una y solo una flecha en la representación gráfica). Y la transformación definida SÍ es una aplicación.

 

Por otra parte, ${{f}^{-1}}(\left\{ 2,3 \right\})$, la imagen inversa de $\left\{ 2,3 \right\}\subset B$, es un subconjunto del conjunto inicial cuyos elementos son todos aquellos elementos de $A$ cuyas imágenes por la aplicación $f$ pertenecen al conjunto $\left\{ 2,3 \right\}$. En la representación gráfica, todos aquellos elementos de $A$ de los que salgan flechas que vayan a parar a cualquier elemento del conjunto $\left\{ 2,3 \right\}$. Luego, ${{f}^{-1}}(\left\{ 2,3 \right\})=\left\{ b,c \right\}\subset A$.

 

Por último, ${{f}^{-1}}(\left\{ 1,3 \right\})$, la imagen inversa de $\left\{ 1,3 \right\}\subset B$, es un subconjunto del conjunto inicial cuyos elementos son todos aquellos elementos de $A$ cuyas imágenes por la aplicación $f$ pertenecen al conjunto $\left\{ 1,3 \right\}$. En la representación gráfica, todos aquellos elementos de $A$ de los que salgan flechas que vayan a parar a cualquier elemento del conjunto $\left\{ 1,3 \right\}$. Luego, ${{f}^{-1}}(\left\{ 1,3 \right\})=\left\{ a,b \right\}\subset A$.